Pascal's Triangle

Pascal's Triangle

At the tip of Pascal's Triangle is the number 1, which makes up the zeroth row. The first row (1 & 1) contains two 1's, both formed by adding the two numbers above them to the left and the right, in this case 1 and 0 (all numbers outside the Triangle are 0's). Do the same to create the 2nd row: 0+1=1; 1+1=2; 1+0=1. And the third: 0+1=1; 1+2=3; 2+1=3; 1+0=1. In this way, the rows of the triangle go on infinitely. A number in the triangle can also be found by nCr (n Choose r) where n is the number of the row and r is the element in that row. For example, in row 3, 1 is the zeroth element, 3 is element number 1, the next three is the 2nd element, and the last 1 is the 3rd element. The formula for nCr is:

n!

--------

r!(n-r)!

! means factorial, or the preceeding number multiplied by all the positive integers that are smaller than the number. 5! = 5 × 4 × 3 × 2 × 1 = 120

The Sums of the Rows:

Sum of  numbers in any row is equal to 2 to the n^th power or 2ⁿ, when n is the number of the row. For example:

2⁰ = 1

2¹ = 1+1 = 2

2² = 1+2+1 = 4

2³ = 1+3+3+1 = 8

2⁴ = 1+4+6+4+1 = 16

Prime Numbers

If the 1^st element in a row is a prime number

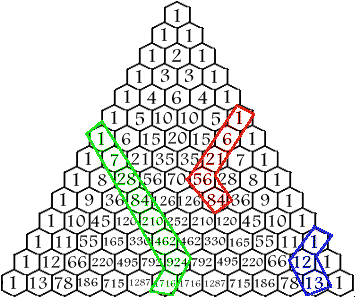
Hockey Stick Pattern:

Diagonal of numbers of any length is selected starting at any of the 1's bordering the sides of the triangle and ending on any number inside the triangle on that diagonal, the sum of the numbers inside the selection is equal to the number below the end of the selection that is not on the same diagonal itself

1+6+21+56 = 84
1+7+28+84+210+462+924 = 1716
1+12 = 13

Fibonnacci's Sequence:

Fibonnacci's Sequence can also be located in Pascal's Triangle. The sum of the numbers in the consecutive rows shown in the diagram are the first numbers of the Fibonnacci Sequence. The Sequence can also be formed in a more direct way, very similar to the method used to form the Triangle, by adding two consecutive numbers in the sequence to produce the next number. The creates the sequence: 1,1,2,3,5,8,13,21,34, 55,89,144,233, etc . . . . The Fibonnacci Sequence can be found in the Golden Rectangle, the lengths of the segments of a pentagram, and in nature, and it decribes a curve which can be found in string instruments, such as the curve of a grand piano.

Hao Xian, Balram, Darryl lam, Enoch, Hao en.