Uses
- It is used in statistics to calculate the binomial distribution.(Probability distribution is the probability distribution of the number of successes in a sequence of n independent in yes/no distribution)
- This allows statisticians to determine the probability of a given number of favorable outcomes in a repeated number of trials.
- Binomial expansion is also interesting from a mathematical point of view--it gives mathematicians insight into the properties of polynomials.
- Used in the distribution of IP addresses
Conceptual aspects
-This is the formula.
How is it used in probability?
- It is used in statistics to calculate the binomial distribution.(Probability distribution is the probability distribution of the number of successes in a sequence of n independent in yes/no distribution)
- This allows statisticians to determine the probability of a given number of favorable outcomes in a repeated number of trials.
- Binomial expansion is also interesting from a mathematical point of view--it gives mathematicians insight into the properties of polynomials.
- Used in the distribution of IP addresses
Conceptual aspects
-This is the formula.
The way to derive the expanded form of a binomial with a exponential e.g. 4.
Lets just have the binomial be (a+b)
(a+b)^3 = a^3 + 3(a^2)b + 3ab^2 + b^3
As can be seen, the a exponents go from 3 to 0. (a^3, 3(a^2)b, 3ab^2, b^3)
The b exponents go from 0 to 3. (a^3, 3(a^2)b, 3ab^2, b^3)
The coefficients go 1,3,3,1 (3rd row of the Pascal triangle)
To get the coefficients, you can use the above formula. Factorial = !
k is the order of the terms (e.g. 2nd or 3rd term)
e.g. to get the coefficient of the 42nd term of a binomial to the power of 50 e.g. ( a+b )^50
50! / (42!)(50-42)! = 536878650
You can get the coefficient of any term using this formula. Used together with the pattern of the exponents of the a and b terms, you can get the expanded form. ( faster than expanding). It is still very slow.
Below is an example of how to use the formula for binomial expansion to get the expanded form of the binomial cubed.
How is it used in probability?
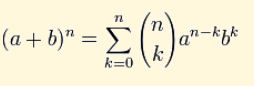




No comments:
Post a Comment