March 27 2013

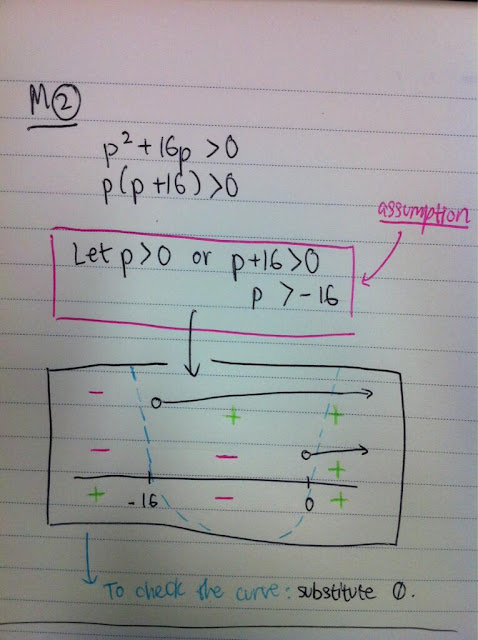
[ Last picture is what we did in the lesson. ]

Retrospective

A term has passed and it is important to take stock of the academic progression.

File Check:
To date I only received 4 files - students who were told to submit their files have not done so. I went to the class on Tuesday and found none.

Consultation:
As promised I have made myself available on Tuesday to assist any students with their work. It was not mandatory however the turnout was rather disappointing - only 3 turned up. I am glad they did as we managed to cover a fair amount of learning.

Their is a dire need to improve on the attitude for some of you. Ultimately it is about your success, your achievement and your future. A teacher is just an agent of change - so just before we embark on another new term please take time to reflect. For those who have done well - kudos and keep it up. For others please shift the gear forward as its time to change.

Lesson summary

Sorry its super late!

Lesson Summary - 13MAR2013

Key learning point(s): Nature of roots

This is determined by the Discriminant (D), which is b^2-4ac, and is also derived from the general formula for Quadratic formulas.

There are three cases:

• When D=0, roots are real and distinct - Graph intersects x-axis twice (Example: x = -2 or 4)
• When D > 0, roots are real and equal - Graph's tangent for turning point is x-axis (Example: x=2)
• When D < 0, roots are imaginary or complex - Graph does not cut x-axis (Example: x=3+4i, x=3+4sqrt-1)

∴ When D ≥ 0, roots are real.

TAKE NOTE:
• When considering whether a variable will result in a positive Discriminant, consider signage! (Example: a^2)
-seen in Pract. 8 (page 157)

Quadratic ... in perpsective

Double period lesson summary - 7/3/13

Try solving this without your calculator
(lg 5)^2 + lg 2(lg 50)

E Maths Paper(First Period)
Remember to attach the weakness/strengths and goals paper behind the paper.

Common errors
Q1. Forgot to simplify
Q2. Overcomplicated the question, wrong assumptions
Q3a. Forgot the +-
Q4a. Multiplication errors
Q4d. No explanation for rejection of answer
Q5c.  Remember brackets for coordinates (Also remember that the graph should cover 75% of the graph paper)
   






Quadratic(Second Period)

Revision

Newer Stuff

D- discriminant derived from quadratic general formula, sqrt(b^2-4ac)


 More Important parts:
x^2-(-b/a)x+(c/a) = 0
x^2-(α+β)x+(αβ) = 0
(-b/a = α+β and c/a = αβ)
 

06/03/13 Lesson

Correct Me if i made any errors thanks.

Summary of Quadratic

 

If by any chance i make a mistake, plus correct me in the comments. Thanks~

REAL LIFE APPLICATION OF QUADRATIC EQUATION

by Mr Johari

source: http://www.mathsisfun.com/algebra/quadratic-equation-real-world.html 

REAL LIFE APPLICATION OF QUADRATIC EQUATION

EXAMPLE 1

Balls, Arrows, Missiles and Stones If you throw a ball (or shoot an arrow, fire a missile or throw a stone) it will go up into the air, slowing down as it goes, then come down again ... ... and a Quadratic Equation tells you where it will be! Example: Throwing a Ball A ball is thrown straight up, from 3 m above the ground, with a velocity of 14 m/s. When does it hit the ground?

Ignoring air resistance, we can work out its height by adding up these three things:

The height starts at 3 m:		3
It travels upwards at 14 meters per second (14 m/s):		14t
Gravity pulls it down, changing its speed by about 5 m/s per second (5 m/s2):		-5t2
(Note for the enthusiastic: the -5t2 comes from -½at2 with a=9.81 m/s2)

Add them up and the height h at any time t is:

h = 3 + 14t - 5t²

And the ball will hit the ground when the height is zero:

3 + 14t - 5t² = 0

Which is a Quadratic Equation ! In "Standard Form" it looks like:

-5t² + 14t + 3 = 0

Let us solve it ...

There are many ways to solve it, here we will use the factoring method:

Will be easier if we multiply all terms by -1:		5t2 - 14t - 3 = 0
Now our job is to factor it. We will use the "Find two numbers that multiply to give a×c, and add to give b" method in Factoring Quadratics. a×c = -15, and b = -14. The positive factors of -15 are 1, 3, 5, 15, and one of the factors has to be negative. By trying a few we find that -15 and 1 work (-15×1=-15, and -15+1= -14)
Rewrite middle with -15 and 1:		5t2 - 15t + t - 3= 0
Factor first two and last two:		5t(t - 3) + 1(t - 3) = 0
Common Factor is (t - 3):		(5t + 1)(t - 3) = 0
And the two solutions are:		5t + 1 = 0 or t - 3 = 0
		t = -0.2 or t = 3

The "t = -0.2" is a negative time, impossible in our case.

The "t = 3" is the answer we want:

The ball hits the ground after 3 seconds!

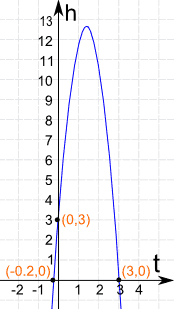Here is the graph of the Parabola h = -5t2 + 14t + 3 It shows you the height of the ball vs time Some interesting points: (0,3) When t=0 (at the start) the ball is at 3 m (-0.2,0) Says that -0.2 seconds BEFORE we threw the ball it was at ground level ... this never happened, so our common sense says to ignore it! (3,0) Says that at 3 seconds the ball is at ground level. Note also that the ball reaches nearly 13 meters high.

Note for the enthusiastic: You can find exactly where the top point is! The method is explained in Graphing Quadratic Equations, and has two steps:

Find where (along the horizontal axis) the top occurs using -b/2a:

• t = -b/2a = -(-14)/(2 × 5) = 14/10 = 1.4 seconds

Then find the height using that value (1.4)

• h = -5t² + 14t + 3 = -5(1.4)² + 14 × 1.4 + 3 = 12.8 meters

So the ball reaches the highest point of 12.8 meters after 1.4 seconds.

===========================================================

EXAMPLE 2

Example: New Sports Bike

You have designed a new style of sports bicycle! Now you want to make lots of them and sell them for profit.

Your costs are going to be:

• $700,000 for manufacturing set-up costs, advertising, etc
• $110 to make each bike

Based on similar bikes, you can expect sales to follow this "Demand Curve": Unit Sales = 70,000 - 200P Where "P" is the price. For example, if you set the price: at $0, you would just give away 70,000 bikes at $350, you would not sell any bikes at all. at $300 you might sell 70,000 - 200×300 = 10,000 bikes

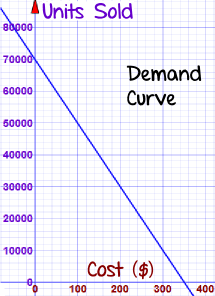So ... what is the best price? And how many should you make?

Let us make some equations!

How many you sell depends on price, so use "P" for Price as the variable

• Unit Sales = 70,000 - 200P
• Sales in Dollars = Units × Price = (70,000 - 200P) × P = 70,000P - 200P²
• Costs = 700,000 + 110 x (70,000 - 200P) = 700,000 + 7,700,000 - 22,000P = 8,400,000 - 22,000P
• Profit = Sales-Costs = 70,000P - 200P² - (8,400,000 - 22,000P) = -200P² + 92,000P - 8,400,000

Profit = -200P² + 92,000P - 8,400,000

Yes, a Quadratic Equation. Let us solve this one by Completing the Square.

Solve: -200P² + 92,000P - 8,400,000 = 0

Step 1 Divide all terms by -200

P² – 460P + 42000 = 0

Step 2 Move the number term to the right side of the equation:

P² – 460P = -42000

Step 3 Complete the square on the left side of the equation and balance this by adding the same number to the right side of the equation:

(b/2)² = (-460/2)² = (-230)² = 52900

P² – 460P + 52900 = -42000 + 52900

(P – 230)² = 10900

Step 4 Take the square root on both sides of the equation:

P – 230 = ±√10900 = ±104 (to nearest whole number)

Step 5 Subtract (-230) from both sides (in other words, add 230):

P = 230 ± 104 = 126 or 334

What does that tell us? It says that the profit will be ZERO when the Price is $126 or $334

But we want to know the maximum profit, don't we?

It will be exactly half way in-between! At $230

And here is the graph: Profit = -200P2 + 92,000P - 8,400,000 The optimum sale price is $230, and you can expect: Unit Sales = 70,000 - 200 x 230 = 24,000 Sales in Dollars = $230 x 24,000 = $5,520,000 Costs = 700,000 + $110 x 24,000 = $3,340,000 Profit = $5,520,000 - $3,340,000 = $2,180,000

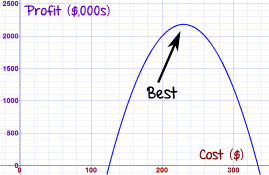A very profitable venture.

===========================================================

EXAMPLE 3

 Example: Small Steel Frame

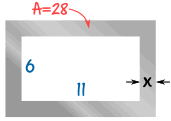Your company is going to make frames as part of a new product they are launching. The frame will be cut out of a piece of steel, and to keep the weight down, the final area should be 28 cm2 The inside of the frame has to be 11 cm by 6 cm What should the width x of the metal be?

Area of steel before cutting:

Area = (11 + 2x) × (6 + 2x) cm²

Area = 66 + 22x + 12x + 4x²

Area = 4x² + 34x + 66

Area of steel after cutting out the 11 × 6 middle:

Area = 4x² + 34x + 66 - 66

Area = 4x² + 34x

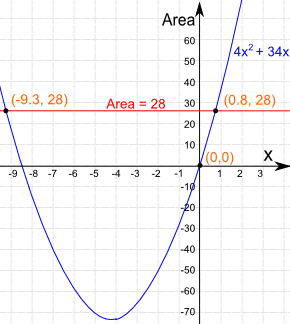
Let us solve this one graphically! Here is the graph of 4x2 + 34x : The required area of 28 is shown as a horizontal line. The area equals 28 cm2 when: x is approximately -9.3 or 0.8 The negative value of x make no sense, so the answer is: x = 0.8 cm (approx.)

===========================================================

EXAMPLE 4

Example: River Cruise

A 3 hour river cruise goes 15 km upstream and then back again. The river has a current of 2 km an hour. What is the boat's speed and how long was the upstream journey?

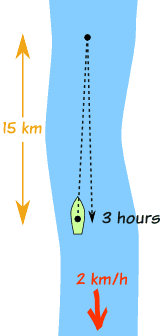There are two speeds to think about: the speed the boat makes in the water, and the speed relative to the land: Let x = the boat's speed in the water (km/h) Let v = the speed relative to the land (km/h) Because the river flows downstream at 2 km/h: when going upstream, v = x-2 (its speed is reduced by 2 km/h) when going downstream, v = x+2 (its speed is increased by 2 km/h) We can turn those speeds into times using: time = distance / speed (if you travel 8 km at 4 km/h it would take 8/4 = 2 hours, right?)

And we know the total time is 3 hours:

total time = time upstream + time downstream = 3 hours

Put all that together:

total time = 15/(x-2) + 15/(x+2) = 3 hours

Now we use our algebra skills to solve for "x".

First, get rid of the fractions by multiplying through by (x-2)(x+2):

3(x-2)(x+2) = 15(x+2) + 15(x-2)

Expand everything:

3(x²-4) = 15x+30 + 15x-30

Bring everything to the left and simplify:

3x² - 30x - 12 = 0

It is a Quadratic Equation! Let us solve it using the Quadratic Formula:

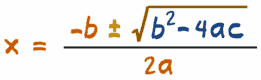
Where a, b and c are from the
Quadratic Equation in "Standard Form": ax² + bx + c = 0

Solve 3x² - 30x - 12 = 0

Coefficients are:		a = 3, b = -30 and c = -12
Quadratic Formula:		x = [ -b ± √(b2-4ac) ] / 2a
Put in a, b and c:		x = [ -(-30) ± √((-30)2-4×3×(-12)) ] / (2×3)
Solve:		x = [ 30 ± √(900+144) ] / 6
		x = [ 30 ± √(1044) ] / 6
		x = ( 30 ± 32.31 ) / 6
		x = -0.39 or 10.39

Answer: x = -0.39 or 10.39 (to 2 decimal places)

x =-0.39 makes no sense for this real world problem, but x = 10.39 is just perfect!

Answer: Boat's Speed = 10.39 km/h (to 2 decimal places)

And hence the upstream journey = 15 / (10.39-2) = 1.79 hours = 1 hour 47min

And the downstream journey = 15 / (10.39+2) = 1.21 hours = 1 hour 13min

Relation Between Roots & Coefficients of Quadratic Equation

by Mr Johari
source: http://www.tutorsonnet.com/math_homework_help/quadratic_equations

Knowing the Quadratic Equation

Part1:  Looking into the Roots and Coefficients of a Quadratic Equation

Part2:  Working backword - how to form a Quadratic Equation if you know the roots.

Revision : Solving Quadratic Equations

by Mr Johari
source: http://www.regentsprep.org/Regents/math

Let us review what has been done in previous 2 years.